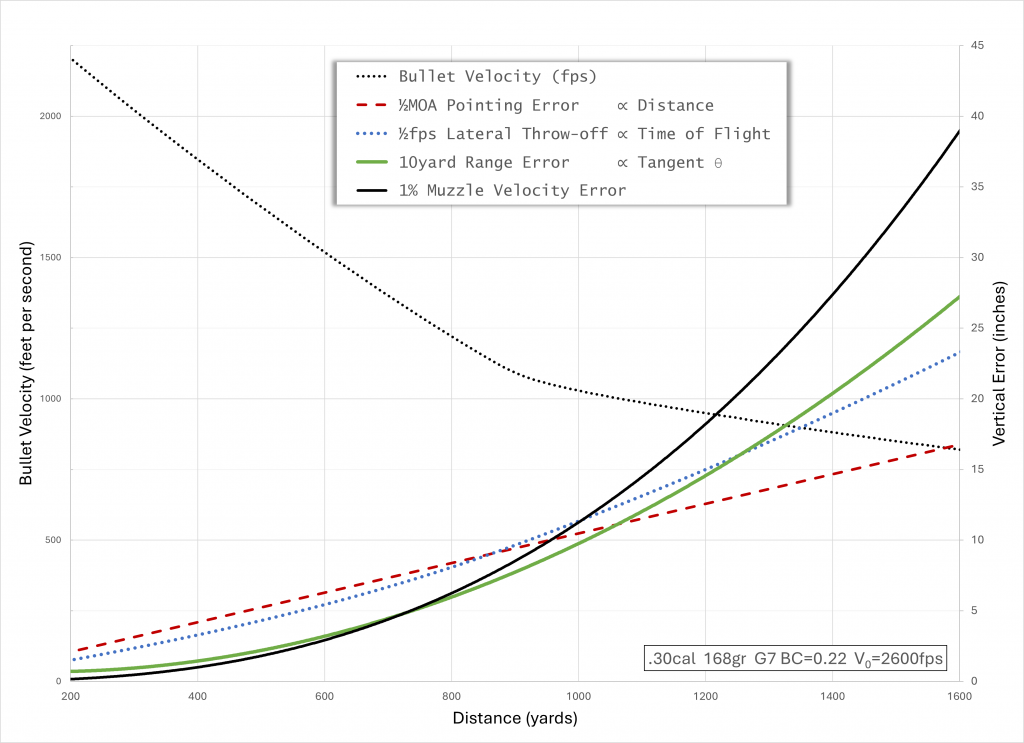
The last post mentioned the standard ballistic drag curves. Here is a chart of them for speeds up to Mach 3:

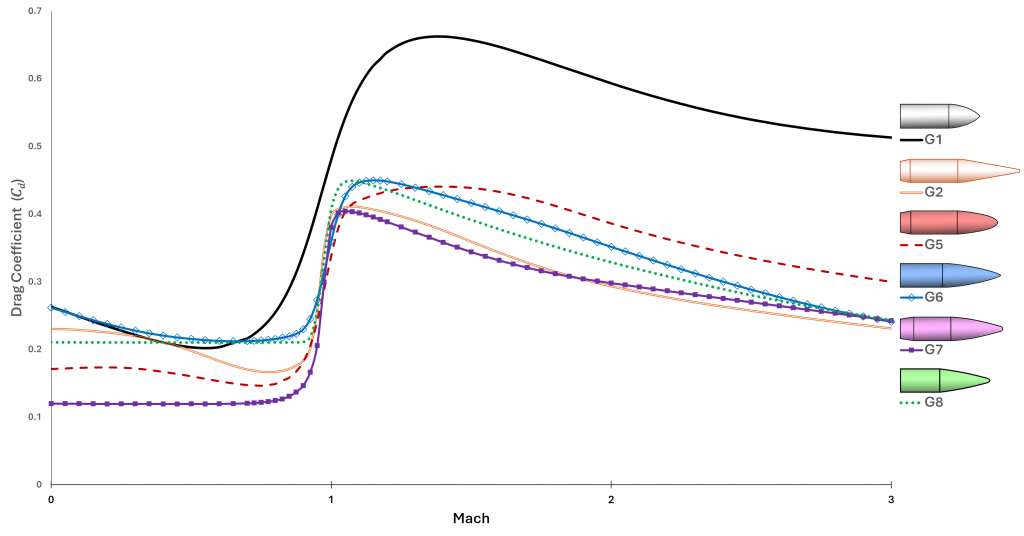
This chart reveals a few quirks of the standard drag models.  First is that G1 is not very precise in the transonic region (i.e., about Mach 1).  The reality of the sound barrier is reflected in the other curves, where drag hits a steep cliff that doubles or triples the subsonic drag coefficient.  The more gentle slope of the G1 curve is a result of 19^th century ballisticians failing to adjust aggregate test data for variations in the speed of sound.

Looking at the low subsonic region we find another strange artifact: several of the curves show an increase in drag as speed goes to zero.  The reality is that drag should be virtually constant across low subsonic speeds.  I asked Jeff Siewert what is going on here and he explained: Back in the day, the test ranges reported what they observed, and at those low speeds the projectiles (especially G2) were likely encountering dynamic instability that increased their yaw.  So those segments reflect an increasing aerodynamic cross-section, not the (constant) drag that would be seen in stable, nose-forward flight.

Example: .308 OTM

Let’s look at a typical rifle bullet: the 168gr .308 BTHP (boat-tail hollow-point), a.k.a. open-tip match (OTM). The profile of this bullet looks very close to the G7 standard projectile, as shown in this image with scaled profiles of the two:

Manufacturers of this bullet still list a Ballistic Coefficient (BC) of 0.462 for use with the G1 drag model. A few decades ago, in an effort to improve trajectory predictions, Sierra published multiple G1 BCs for different velocity ranges: 0.462 above 2600 fps, 0.447 above 2100 fps, 0.424 above 1600 fps, and 0.405 below that. Eventually Berger began to publish G7 BCs, and this bullet is often quoted with a G7 BC of 0.224. A decade ago Bryan Litz began publishing detailed drag models for rifle bullets. For Sierra’s version of this bullet he lists multiple G7 BCs: 0.226 above 3000fps, 0.222 at 2500fps, 0.214 at 2000fps, and 0.211 below 1500fps. Here is a chart of the drag curves resulting from each of these variations:

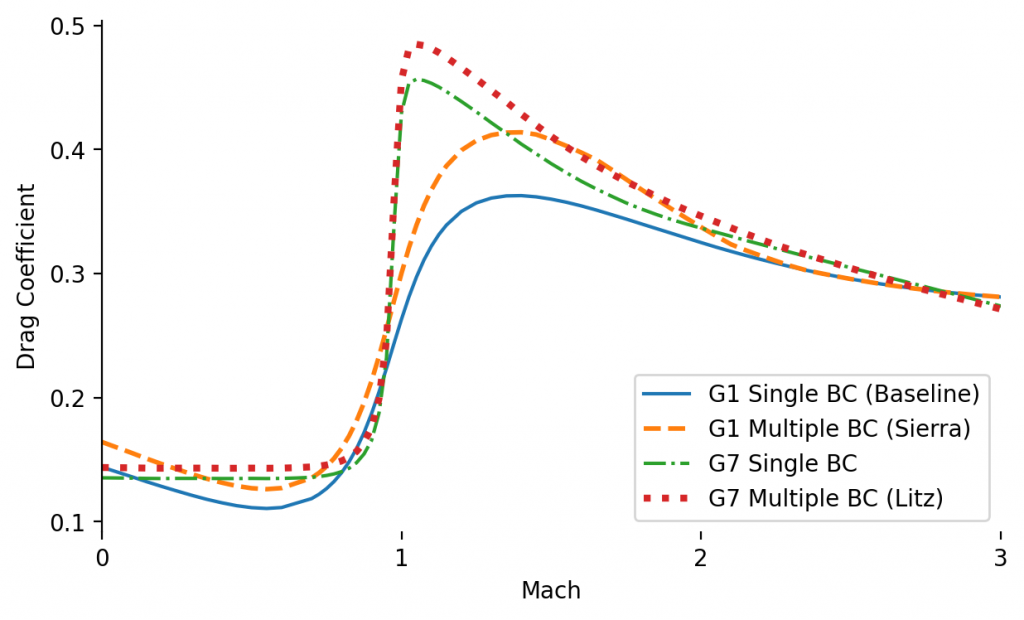
Long-Range Consequences

How meaningful are these differences? I ran the trajectory for each model using a muzzle velocity of 3000fps, zeroed at 500 yards. Here are the drops on the baseline (G1) trajectory, and then the additional drop when using each of the other drag curves:

	Baseline (G1)	Drop: Difference from Baseline
Distance (yards)	Drop (inches)	G1 Multi	G7	G7 Multi
500	0	0.1	0.6	0.6
1000	233	8.7	10.3	16.3
1500	962	78.5	95.9	142.5

So there’s not a meaningful difference until we’re looking at ranges closer to 1,000 yards. At longer ranges, however, the vertical error from the inferior models is measured in feet!

Minimizing muzzle velocity variance is a key to long-range shooting precision. The following chart (taken from my forthcoming book) shows the downrange effects of typical sources of vertical error in a typical .30 caliber rifle shot. In this example, the change in vertical impact caused by a 1% change in muzzle velocity is negligible at shorter ranges, but after 1000 yards it dominates the other sources of error:

What causes muzzle velocity variance, and what can we do to reduce it? One obvious source is variation in powder charge weight. Within the range of safe powder charges, muzzle velocity shows a linear increase with the mass of powder. So precision loaders meter powder charge weights to hundredths of a grain. But even after eliminating any measurable variation in the weight and dimensions of cartridges, it is not uncommon to find the standard deviation of muzzle velocity running up to 1%.

What else is there? Jeff Siewart has identified variation in engraving force¹ as a significant source of variation in muzzle velocity. What is engraving? Here are pictures of bullets, before and after being fired through a rifled barrel:

As a bullet enters a rifled barrel it has to engage and follow the rifling so that it gets spin stabilized. Engraving refers to the raised steel rifling of the barrel scraping into the surface of the bullet, as well as the entire circumference of the bullet deforming to create a tight seal with the barrel to keep the propellant gases from blowing past the bullet. Siewart has shown that the friction involved in engraving varies enough from one shot to another to cause the variations observed in muzzle velocity.

This engraving friction becomes even more significant in subsonic rifle rounds because (a) they are longer, which increases the surface area that must be engraved; and (b) they are fired at lower pressures and velocities, so the same variations in engraving force are a larger proportion of the total internal ballistic impulse.

Can we reduce friction?

There are two established ways of reducing friction between bullet and bore. One is to reduce the bearing surface area of the bullet that contacts the barrel. A notable example of this approach was the addition by Barnes Bullets of cannelures to its solid copper bullet, which markedly increased its shooting precision.² The following photo shows how these cannelures reduce the engraved surface area (as well as providing more relief for material displaced by engraving):

The other method of reducing friction is lubrication. Ten years ago I did extensive testing of various bullet and barrel lubricants in subsonic .30 bullets. Some of these did measurably reduce friction and improve shooting precision: Rydol’s “polysonic” treatment and Dyna-Tek’s “Nano-Ceramic” coating. Impact-plating with hBN (hexagonal boron nitride) did not. This is described in detail here. I didn’t test but would also expect the established MoS₂ (“moly”) and WS₂ (tungsten disulfide) bullet coatings to produce the same benefits.

---

¹ See §Peak Engraving Pressure Variation, p.5 in November 2023 paper, “Using an Error Budget Approach to Estimate Muzzle Velocity Variation.”

² See pp.4-6 in December 2020 paper, “What causes Dispersion.”

I have spent a lot of time testing the precision of common firearms. As I have been explaining for years, it takes a lot of shots to get statistically significant measurements of precision. And I wanted to be able to collect large samples without wondering whether I as a shooter was introducing variance in the results.

In order to remove the shooter from the equation, precision ballistics researchers going back as far as Franklin Mann in the late 1800s have used “V rests” to clamp barrels to benches.  I wanted to do the same, but with a wide variety of modern firearms, and without disassembling them. So ten years ago I built two “test rigs” with the following design objectives:

1. Securely hold any gun with a scope rail;
2. Allow the gun to be loaded, unloaded, and fired while attached;
3. Precisely return the firearm to the same zero after every shot.

Here are photos of the first version:

With a gun clamped in the fixture, I can precisely align it with the same point on the target for every shot, and then fire it while touching only the trigger. Both versions consist of:

1. A Lower Frame supported on the bench with three Screws to fine-tune the point of aim.  To maximize their turning precision, the inserts use class 3 threads, and the end of each screw is turned to a sharp point.  The Lower Frame is tall enough to hold any man-portable gun with a magazine inserted.
2. Two chrome-plated 12mm linear rail Shafts clamped to the Lower Frame.
3. Two linear ball bearing Bushings on each Shaft.
4. Springs that fit over the Shafts to absorb recoil of the Upper Bracket.
5. An Upper Bracket, H-shaped, that screws into the Bushings.
6. A Scope Rail on top of the Upper Bracket, to which I fixed a scope with up to 32x magnification.
7. In the center of the Upper Bracket are two side Clamp Plates with a V channel cut along their length for gripping the scope rail of any gun to be tested.  One of the Clamp Plates rides on pins with springs, and is pushed by a Camming Lever to quickly clamp and release the guns.

The second version of the fixture added threads on top of the Upper Bracket for attaching up to 20 pounds of weight to dampen recoil, as well as a tray in the front that held up to 40 pounds of lead to keep it from lifting off the bench when shooting .308 rifles.