The .45 ACP cartridge has a strange, cult-like devotion among many American handgunners. Strange because it is practically inferior to more modern pistol cartridges. Its diameter makes it impractical for double-stack magazines (which is not to say those don’t exist: I handled FN’s double-stack FNP-45 but it is far too large for a carry gun), which means capacity is typically just 8 rounds for a full-sized gun. The chamber pressure limit for the cartridge is just 21kpsi, vs. 35-40kpsi for more modern pistol cartridges. This may have been a benefit in the past but with the ubiquity of strong alloys and precise manufacturing technologies it is no longer. It does, however, mean that the cartridge is optimized for propelling heavier bullets at slower velocities, which as I explained in a previous post results in more recoil for a given level of energy. Finally, the heavy bullets and larger dimensions of the cartridge make it significantly more expensive than other defensive pistol cartridges.
The .45 ACP was developed and launched along with the 1911 pistol, so even though 1911s are produced for other calibers there seems to be some nostalgia for shooting 1911s chambered in .45 ACP. But there is also a great deal of lore surrounding the prowess of the cartridge as a “man-stopper.” This is almost certainly rooted in the military’s experience with pistols. The U.S. has followed the 1899 Hague Convention, which prohibits the use of hollow-point bullets in warfare. Until 2010 even military police carried full metal jacket pistol loads. Rifle bullets go fast enough that standard copper jackets break up in soft tissue, creating large wound channels and dumping most of their energy into human targets. But slow, solid handgun bullets punch through human targets practically intact, which means that they leave a wound channel only as wide as the bullet itself. Given this constraint it’s not surprising that .45s developed a reputation for stopping people with fewer shots than smaller bullets that have been government issued.
But this situation does not apply to civilians, who can carry hollow-point bullets. The standard test for terminal ballistic performance is to shoot gelatin that is calibrated to the consistency of animal tissue. The following image shows the wound channel and penetration of standard loads using jacketed hollow-point (JHP) bullets:
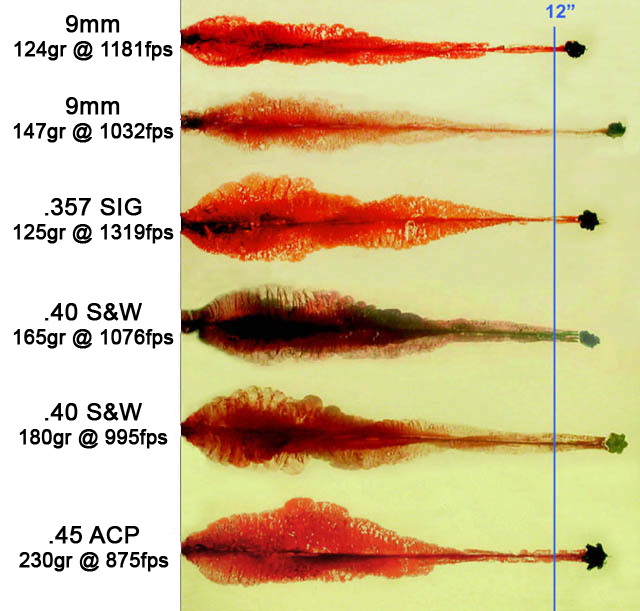
With hollow-point bullets the .45 ACP offers no advantage in stopping power over .40 S&W or .357 SIG (my favorite), which have the advantages of lower recoil, lower cost, and higher magazine capacities.
| Caliber | Bullet Mass |
Muzzle Velocity |
Muzzle Energy |
Power Factor |
Relative Energy |
Relative Recoil |
|---|---|---|---|---|---|---|
| 9mm | 124gr | 1181fps | 384ft-lbs | 146 | 1.10x | 1x |
| 9mm | 147gr | 1032fps | 348ft-lbs | 152 | 1x | 1.04x |
| .357 SIG | 125gr | 1319fps | 483ft-lbs | 165 | 1.39x | 1.13x |
| .40 S&W | 165gr | 1076fps | 424ft-lbs | 178 | 1.22x | 1.21x |
| .40 S&W | 180gr | 995fps | 396ft-lbs | 179 | 1.14x | 1.22x |
| .45 ACP | 230gr | 875fps | 391ft-lbs | 201 | 1.12x | 1.37x |
One obvious question is why no .45 cartridge has been specified with higher pressure limits? For example, raising peak pressure to 32kpsi could add 200fps to the load shown here, boosting both Relative Energy and Relative Recoil to 1.7x. One obstacle may be the popularity of 1911 .45s: Neither a standard 1911 nor a standard .45 ACP case can safely support much higher pressures. A few wildcat cartridges have emerged over the years (e.g., .45 Super and .450 SMC) with the same external dimensions and higher pressures, but SAAMI will probably not approve any such cartridges because they could be inadvertently fired in a .45 ACP gun, causing damage and potentially catastrophic failure. SAAMI did approve the .45 Win Mag because its slightly longer cases wouldn’t chamber in a .45 ACP. However that caliber never really caught on, perhaps due to the other problem: power factors above 250 represent a level of recoil that is apparently not practical for a defensive carry pistol.
I recommend this page for further reading on terminal ballistics.
Firing a Sig handgun with the .357 Sig is the best experience you can have with a handgun — as noted in an earlier post, a Sig is like a fine watch. All the more so when you take into account what is demonstrated here: the fact that it has the highest energy and lowest recoil relative to energy of the popular rounds (and maybe the less popular as well).
In all those ballistic gel pictures, the fact is they can fail to expand. This is particularly so in the case of short barrel revolvers were . In fact, a pistol shot of a .22 Stinger penetrates over 18 inches because it fails to expand, yet is less than 12 inches when forced to expand by hypersonic velocities. A .45 never shrinks and has a larger wound channel at the same velocities.
Also, it is difficult to get a .357 in any firearm that has more than 8 shots. Furthermore, you are comparing the 230 grain round with the lighter rounds of the others. Velocity is far more important than weight in the foot pounds formula. If you are going to host foot pounds as the most important figure, then the .45 ACP +P Remington Golden Saber JHP Bullet 185 Grain 1140 fps cartridge is the fair comparison.
Muzzle velocity: 1140 fps.
Velocity at 50 yards: 1040 fps.
Muzzle energy: 534 ft/lbs.
Energy at 50 yards: 446 ft/lbs.
Real “stopping power” is demonstrated on the autopsy table. It has proven itself for over a century in practice, mostly at subsonic velocities where a .45 ACP can be silenced and still remain effective. Regarding higher pressures, you should consider the shotgun. A 10 gauge 3.5 inch shell has more power than any handgun under 50 yards. A 20 gauge 3″ shotgun is more powerful than a .357. An Ammo 20 Gauge Brenneke USA Magnum 3″ Rifled Slug Lead 1 Ounce clocks at 1476 fps with 2114 foot pounds.
John: Some good points. Yes, for subsonic shooting velocity is capped, so the only way to get more energy is to increase bullet mass. However “modern-pressure” cartridges can still outdo the .45 ACP, able to shoot heavier bullets at closer to the 1000fps ideal for subsonics.
It might be more fair to look a the lightest .45 bullets for this comparison. However in this analysis none of the loadings were +P spec. (Besides which I see far fewer .45’s rated for +P than guns in the more modern chamberings.)
My understanding is that the latest generation of expanding bullets are extremely reliable, even from short barrels, and even through barriers that often “clogged” older hollow points.
Peak pressure isn’t the only factor; as you note shotguns typically don’t exceed 12kpsi but put out far more energy than handguns. But when we confine the discussion to handguns (i.e., short barrels) it’s clear that peak pressure is a dominant constraint.
You are still maintaining .45 ACP is obsolete, I take it. The .22 has been around since 1847 and the .22 LR since 1887. Leaving out rifles and shotguns, a .22 requires fewer rounds to incapacitate a person than any of those rounds you list and you will find a .22LR CCI stinger from a short pistol penetrates further than any of those rounds you show. SEE:
http://www.buckeyefirearms.org/handgun-stopping-power
http://www.youtube.com/watch?v=U2PSddmxGtI 13″ penetration
https://www.youtube.com/watch?v=gbVY4gT5P20 13″ to Over 16″ penetration with .22LR
http://www.youtube.com/watch?v=hUOGNq_iF2A
http://www.youtube.com/watch?v=2T10BMy6oq0
40S&W Federal 165gr Tactical HST in Ballistic Gelatin
http://www.youtube.com/watch?v=OUx1aIb2cWs
http://www.youtube.com/watch?v=z1DeT4hana0
Speer Gold Dot .40 S&W 180 gr JHP SIM-TEST w/denim
http://www.youtube.com/watch?v=39NDONv3MQY
http://www.youtube.com/watch?v=Wuz_RHkS0aU
So, energy and bullet mass have nothing to do with penetration and I would submit penetration has nothing to do with stopping power, unless you hit the most vital organs in the body, the small node of the heart that keeps its rhythm or the medulla oblongata of the brain controlling movements in the body. For accuracy in head and torso hits, none of the rounds shown match the .45 ACP, referring to the stopping power article.
45acp–Vs–9mm—-BALLISTICS GEL TESTING
http://www.youtube.com/watch?v=eJKZO71mEns
Hornady XTP .45 ACP +P 230 gr JHP AMMO TEST
http://www.youtube.com/watch?v=3Ct33tKvpKo 14.75 inches
Hornady Critical Defense .40 S&W 165 gr FTX: SIM-TEST* w/denim 15.0 inches
http://www.youtube.com/watch?v=tkOV3MJI1FU
.45 ACP +P Hornady XTP 200 gr JHP Gel Ammo Test 17.75 inches penetration
http://www.youtube.com/watch?v=Pl_anGfqnAI
Your claim that “modern pressure” cartridges can outdo the .45 ACP is not the cut and dried absolute you declare. I don’t think you can argue against the proven history of the .45 ACP and the fact it has such a long history of reliability makes it popular. It is not sentimental nostalgia, but trust that propels that. SEE WHERE IT STARTS:
The Thompson-LaGarde Report
http://unblinkingeye.com/Guns/TLGR/tlgr.html
To my knowledge, you would be hard pressed to find a .45 ACP that is NOT +P manufactured within my lifetime. I do not recommend +P as a target practice round in anything.
I don’t see on what you’re basing your assertions that “a .22 requires fewer rounds to incapacitate a person than any of those rounds you list” or, “For accuracy in head and torso hits, none of the rounds shown match the .45 ACP.”
Your first link, An Alternate Look at Handgun Stopping Power by Greg Ellifritz, is the best single reference I would use for discussions of “stopping power” — i.e., effective terminal ballistics. See my summary of relevant conclusions in this post.
You can get all sorts of terminal effects — deep penetration with small wound channels, or shallow penetration with a large wound cavity — by tailoring bullet design. The current accepted wisdom is that the best handgun bullet for stopping unarmored humans is one that penetrates at least 12 inches in ballistic gel and no more than 18 inches, and that delivers as much kinetic energy as possible without reducing the ability of the shooter to make rapid and accurate shots. Almost every cartridge/gun combination can be tuned to that penetration region, so the differences that appear in wound cavity are directly correlated to kinetic energy. (Note that we’re leaving out a secondary ballistic objective, which is the ability to penetrate and resist deflection of barriers. This is a separate and substantial subject of constant R&D. Suffice it to note that mass and velocity for this purpose are good, while larger diameters are bad, so on net the .45 doesn’t stand out here either.)
So yes, the .45 ACP is obsolete because it delivers less energy with more recoil than higher-pressure rounds. The fact that it has a proven history is mostly irrelevant because, as I explain in the beginning of this article, this history and reputation was built during periods and circumstances where shooters could only use non-expanding bullets.
Finally, given how long the 1911 design has been in production, I would wager that the odds of any working 1911 in .45 ACP being +P safe are not in your favor. Even many of modern manufacture specify a heavier recoil spring when shooting +P .45 ACP.
First, large diameters are not bad and a heavier recoil spring does not seem related to the issue of chamber pressure. I do not see where you have any evidence to the contrary. I do not anticipate any firearm with over 50 years of use disappearing in the next 100 years.
You have made your argument. I have made mine. My last point is no firearm is a one-shot-one-kill without daily training with firearms and great physical shape. If you can afford to do that, then your 40 or 9 is adequate. Short of that, if you examine the stats, unless you shoot them three times, then you are going to fail to stop them more often than not.
My rule is three yards, three seconds, and three shots. Any firearm is equally able to accomplish the task of disabling an intruder regardless of whether it is a .22 or a .460 or whether it is 1911 or 2111. It issue really comes down to recoil and confidence enough to maintain accuracy in the high pressure of the event – not the firearm. My evidence proves the points I made.
If we’re considering the .45 acp to be an obsolete round simply
because of age, then the 9 mm should be considered even more obsolete.
616 ft/lbs.45 ACP Bonded Match Hollow Point Atomic Ammo 16 in. penetration.
899 ft/lbs .45 ACP +P MagSafe Defender Frangible 96 Grain Bullet 1660 fps
You’d be hard pressed to find a 9mm cartridge above 520 ft/lbs or a JHP with 16 inches of penetration.
Of course, Ben Martinez, as you say, the 9mm was designed 2 years before the .45ACP.
Federalist, using the data of Ellifriz.
PERCENT INCAPACITATED BY ONE SHOT TO TORSO OR HEAD:
47%-9mm Lugar
49%-.25 ACP
51%-.45 ACP
52%-.40 S&W
53%-.44 Magnum
55%-.38 Special
60%-.22 Short, Long, and Long Rifle
61%-.357 Magnum and Sig
62%-.380 ACP
72%-.32
80%-All Center Fire Rifles
86%-Shotguns, 90% of which were 12 gauge.
Number of Rounds To Incapacitate:
2.45 rounds-9mm Lugar
2.36 rounds-.40 S&W
2.20 rounds-.25 ACP
2.08 rounds-.45 ACP
1.86 rounds-.38 Special
1.76 rounds-.380 ACP
1.71 rounds-.44 Magnum
1.70 rounds-.356 Magnum or Sig
1.52 rounds-.32
1.40 rounds-typical center fire rifle
1.38 rounds-.22 LR, Long, or Short
1.22 rounds-typical Shotgun, 90% of which are 12 gauge
Obviously, the fewer rounds it takes to incapacitate, the better.
Your assumption seems to be based entirely on this slim difference:
Percentage of People Not Incapacitated
40%-.32 Long, ACP
35%-.25 ACP
31%-.22 LR, Long, Short
17%-.38 Special
16%-.380 ACP
14%-.45 ACP
13%-9mm Lugar
13%-.40 S&W
13%-.44 Magnum
12%-Shotgun(All, 90% 12 Gauge
9%-.357(Magnum & Sig)
9%-Rifle(centerfire)
I have to wonder if “failure to incapacitate” includes those who run away – likely to need hospitalization or die later.
MOST IMPORTANTLY, you cannot base performance standards based on that single image of cherry picked rounds.
Your claim about the efficiency of the ballistics is proven wrong, obviously. That includes your claim about reliability of the 9mm in expansion.
Your other claims about recoil seem not to be backed by data. Nor is it as simple as you seem to think, but this is rule of thumb calculator.
http://www.handloads.com/calc/recoil.asp
A great deal depends on the design of the weapon with such features as the combination of slide weight/spring, style of grip, and the porting of the barrel.
Regarding what is carried by regulation, it was found the 9mm was ineffective compared to the .45 ACP by the marines, who have ordered replacements. The problem was over penetration with ball rounds by the 9mm, delivering less energy/trauma to the aggressor.
http://www.defensemedianetwork.com/stories/the-return-of-the-m1911-45-acp/
What we know is a .45 ACP will not shrink to 9mm if it fails. However, I have a comparison of ammo- same manufacturer/+P – a fair comparison.
Speer Gold Dot 9mm +P 124 gr JHP SIM-TEST w/denim
.614 Average expansion
13.5 in penetration
http://www.youtube.com/watch?v=fdXfDcY-0gU
.45 ACP +P Speer Gold Dot 200 gr JHP Gel Test
.787in. Average
12.75 in penetration
To restate my thesis more succinctly: The .45 ACP is obsolete because, of all common auto-loading defensive handgun rounds, it:
John, I don’t see how your reply rebuts any of my claims.
Yes, it’s not hard to find .45 ACP cartridges that deliver more energy than 9mm cartridges, and more energy will typically deliver greater penetration and/or larger wound cavities. But in .45 ACP you always pay a (large) price for that (small) advantage in terms of recoil, capacity, and weight.
The calculation of recoil is straightforward: it is directly proportional to mass times muzzle velocity. (You can pick your units, but for relative comparisons they don’t matter.) It is true that “felt recoil” is subjective and depends on many factors. But .45 ACP has the highest physical recoil, so holding all else constant (which you can actually do for many guns which can be chambered in every round considered here) it will also have the highest felt recoil.
I specifically point out that in the unique case of armed forces who have to carry non-expanding ammunition the larger diameter of a .45 is an obvious advantage in terms of terminal ballistics. Of course 9mm hardball, being smaller diameter and higher velocity, will tend to overpenetrate and deliver smaller wound channels.
For everyone else: You allude to failures to expand. My impression is that this is no longer a serious concern with state-of-the-art expanding bullets. If you have data to the contrary that would be relevant.
I have made a more than adequate argument with a detailed explanation.
Sorry, I’ve reread your comments, your blog post, and Ellifritz, and I’m not seeing it. Can you summarize which data prove my claims about ballistic efficiency to be wrong? (I’m assuming your example of a gel test on two Gold-Dot loads was not it, since the gel results were pretty close even though you chose the weakest cartridge in the lineup.)
I chose two videos of the same brand and same type defense loads to show penetration.
They are not “the weakest [9mm] cartridge” It is a fair comparison.
I also chose some of the best examples of each before of energy for loads and the .45 is more than sufficient.
If you have a 9mm round with better performance than these, show them:
616 ft/lbs.45 ACP Bonded Match Hollow Point Atomic Ammo 16 in. penetration.
899 ft/lbs .45 ACP +P MagSafe Defender Frangible 96 Grain Bullet 1660 fps
As I pointed out, your claims about recoil are not backed by data.
You say, “Delivers less energy per unit of recoil.”
You produced no data to prove that.
From the blog data, the .45ACP performed better:
PERCENT INCAPACITATED BY ONE SHOT TO TORSO OR HEAD:
47%-9mm Lugar
51%-.45 ACP
Number of Rounds To Incapacitate:
2.45 rounds-9mm Lugar
2.08 rounds-.45 ACP
Personally, I even prefer my PK380 to a 9mm for my concealed carry.
I can accept your preference for a 9mm, but by no means is a .45 obsolete and one can easily make a case for it over the performance of a 9mm.
But you keep making the same arguments and discounting the facts, which I presented in several posts.
Again, I had already made a more than adequate argument with a detailed explanation.
Thanks, I see what you’re referring to.
Your examples of high-energy loads .45 require this caveat: 616 ft/lbs is from a 185gr bullet, which is light for caliber. If you take comparably light-for-caliber bullets in the other calibers you will see proportionally higher muzzle energy. Ultra-light bullets like the 96-grain .45 bullet do not meet the criteria for defensive rounds because they lack penetration. (They can make an impressive balloon in the first few inches of a gel block, but any advertising to the contrary I am not aware of any authority that would recommend such bullets for defense against humans or large animals.) Their external ballistics are also terrible because their sectional density is so small.
The table in my initial post provides the data on energy per unit recoil: just take the ratio of the last two columns. Using those cartridges the highest energy per recoil is the .357 SIG at 1.2; the lowest is the .45 ACP at 0.8. No other cartridge scores below 0.9.
The differences you cite from Ellifritz on “percent incapacitated by one shot” are not statistically significant, and as Ellifritz noted that’s obviously not the right statistic to look at when considering cartridge efficiency since calibers considered too weak for reliable defense (like .22LR) score even higher. Ellifritz also noted that “number of rounds to incapacitate” more likely reflected the average capacity of guns and number of rounds discharged per shooting, since once again weaker revolver rounds appear to outperform more powerful autoloaders. (And of course the highest-capacity guns tend to be 9mm autoloaders.)
You claim the ultralight round lacks penetration without the slightest shred of evidence.
You evaded the challenge as stated, which was to come up with a 9mm round with the equivalent energy even for the 185 grain bullet. The fact that it is “light for caliber” is totally irrelevant. It is still heavier than a 9mm round, which is part of the argument. I am not willing to address those other issues. Find a 9mm round with that kind of energy and momentum that cartridge offers. In fact, I doubt you can find a 9mm with the 16 inches of penetration the 616 ft/lbs.45 ACP Bonded Match Hollow Point Atomic Ammo has.
I suspect only BALL ammo has the penetration you claim once you pass it through 4 layers of denim. Penetration depends on momentum.
This these are .45 ACP HP rounds compared.
http://www.youtube.com/watch?v=nt43BScUdt0
These are a series of comparisons of 9mm Vs. .45 ACP using the same brand ammo for comparison with 20% rather than 10%:
http://www.youtube.com/watch?v=6CGWvJOXP9k&list=PL3F37FF69375FAD3C
You are still are 166 ft pounds below the round I cited. That is far below “about the same.”
http://www.atomicammunition.com/45acp185.html
I’m saving the ultralight terminal ballistics for another post. [Update: Here it is.]
Atomic’s 185gr .45 figures are from a 5″ barrel. I don’t have any 5″ 9mms, and I can’t find any chronograph data for one, but for reference CORBON makes a 90gr 9mm that does 450 ft-lbs out of a 4″ barrel. If you use the same barrel length you will find muzzle energy from 115gr and lighter 9mm +P to be about the same as the 185gr .45 +P.
If you want penetration any 9mm hardball will shoot clear through a standard 16″ block. I recall it takes almost two feet of gel to stop those. As I mentioned before, bullets can be tailored within a wide range of expansion and penetration profiles.
Note also, the 9mm is the lowest-energy cartridge of the canonical defensive-grade autoloader rounds. The fact that this smaller, cheaper round can contend with .45s is part of what renders the latter obsolete. Compare to my preferred cartridge, the .357 SIG, and there’s no contest.
Sorry about you luck with those short 9mm barrels.
I suspect you will find they weigh more than a .45ACP in most cases.
This is a totally unsupportable statement:
“If your preference is for big, heavy-recoiling cartridges that punch big entry holes, wouldn’t you prefer 10mm, .50AE, or others that do so with notably more energy per unit recoil than .45 ACP?”
The .45ACP runs from 6.8 to 7.9 ft./lbs of recoil with easily a bottom of 616 to a top of 899 foot pounds of energy.
The 10mm nominally is 11.4 ft./lbs of recoil with just 624 foot pounds of energy.
The .50 AD is 25 to 29 ft/lbs of recoil with 1208 to 1478 foot pounds of energy.
TO COMPARE THE RECOIL OF A SHOTGUN:
.45ACP is in the range of a .410 bore
10mm is in the range of a 20 gauge
.50 AE is in the range of a 12 gauge
TO COMPARE ENERGY:
The .45ACP exceeds the energy of a .410 bore slug.
The 10mm has less energy than a .410 bore slug.
The .50 AE has less energy than a 20 gauge.
Given the 9mm having about 53% of the capacity for powder of a .45, most of its pressure rating of 34,000 PSI is wasted.
While the SAAMI rating of the .45 ACP is only 21,000, it is 50% more than the 14,000PSI of the 12 gauge 3.5 inch shell.
The 1.375 oz slug of a 3.5 inch shell with 4759 ft/lbs of energy, comparable with a 500 Linebaugh in recoil at 1741 ft./lbs.
The interesting thing is I have said nothing about a preference for large cartridges. That seems to be a personal attack. You assume far too much without getting the facts. My concealed carry weapon is a PK380. I find it adequate and with a history performance better than the 9mm, even though it has the same size bullets and less energy.
My point is the .45ACP just is NOT “obsolete.” It out performs the 9mm in stopping power and accuracy at self defense ranges. I think it has a great deal of untapped power for the future where improvements can be made.
45 Auto+P 230 gr HP XTP® TAP® FPD™
950fps/461ft./lbs. 19.25 penetration
Expansion to .652 in.
9mm +P Federal HST 124 gr Ammo Test 4″ barrel
1178 fps/382 ft/lbs 14.75 in. penetration
Expansion to .591
Remington Golden Saber .45 ACP 230 gr JHP SIM-TEST w/denim 5″ barrel
860fps/378 ft./lbs 14 in. penetration
Expansion to .704 in.
John: These are more reasonable comparisons, but they would be even better if barrel lengths were identical.
Is your implied argument that the measured terminal ballistics advantage of the .45 ACP over 9mm outweighs all of the comparative disadvantages I described?
9mm +P Federal HST 124 gr $20.99=$1.05/round
http://www.midwayusa.com/product/163019/federal-premium-personal-defense-ammunition-9mm-luger-124-grain-hydra-shok-jacketed-hollow-point-box-of-20
Remington Golden Saber Ammunition 45 ACP 230 Grain Brass Jacketed Hollow Point $36.49=$1.46/round
http://www.midwayusa.com/product/172982/remington-golden-saber-ammunition-45-acp-230-grain-brass-jacketed-hollow-point-box-of-25
9mm case capacity=(13.30 gr H2O)0.862 cm3
Max.Pressure=235.00 MPa (34,084 psi)
.45 Case capacity=(25 gr H2O)1.6 cm3
Max.Pressure=140 MPa(21,000 psi)
I am not going to go any further than to say there is no “comparative advantage” with the 9mm nor that the .45ACP is anywhere near “obsolete” and stick to the point.You are still are 166 ft pounds below the round I cited for the muzzle energy. You cannot even admit that.
616 ft/lbs.45 ACP Bonded Match Hollow Point Atomic Ammo
$49.19/50 rounds= $.99/round
http://www.cheaperthandirt.com/product/AMM-572
I see no “comparative advantage” with the 9mm nor that the .45ACP is anywhere near “obsolete”, but let’s stick to the point.
You are still are 166 ft pounds below the round I cited for the muzzle energy.
I never claimed every other caliber could meet or exceed the energy or expansion diameter of any .45 ACP loading — although the fact that the smallest, with half the case capacity, can put out 75% of the energy of your favorite example with 80% of the barrel length strikes me as impressive.
What makes the .45 ACP obsolete are the points summarized earlier: Whatever your objective, there are more modern (i.e., higher-pressure) auto-loading pistol cartridges that are better. Whether it’s penetration, muzzle energy, cost, magazine capacity, or recoil, almost any of the alternatives mentioned are clearly better across the board. The weakest of the bunch (9mm) is better in almost every regard, and on balance I believe is clearly preferable.
If your preference is for big, heavy-recoiling cartridges that punch big entry holes, wouldn’t you prefer 10mm, .50AE, or others that do so with notably more energy per unit recoil than .45 ACP?
I get the sense you have failed to grasp the physics or fundamental points of my arguments. There is no characteristic of the .45 ACP that can not be significantly exceeded by higher-MAP cartridges, with the sole exceptions perhaps being that, due to its age, there might be more autoloading pistols chambered for it in circulation than for any other defensive caliber, and because of its low MAP they can be made from lower-quality alloys.
The numbers you have put out recently are inaccurate and/or misleading. Units for recoil are lb-ft/s, not ft-lbs. The figures you quote for the .45 ACP are wildly optimistic and apparently given without regard to barrel length, which is essential to any comparison. If you want to compare recoil and energy use the same barrel lengths and same side of the loading range (i.e., lightest bullet for caliber or heaviest). One suggestion: Look at the loads from one manufacturer since any bias in claimed performance is probably carried across their product line. For example, I referenced CORBON earlier. Any fair comparison will clearly show the .45 ACP providing less energy per unit recoil than higher MAP cartridges. That’s physics, and all the marketing or cherry-picked examples in the world can’t negate it.
You won’t see “future improvements” in .45 ACP because it’s hamstrung by its construction, which is what also ties it to such low MAP. If you want to duplicate the .45 ACP ballistics in a more efficient package there’s .45 GAP. If you like the .45 ACP package you can duplicate it or load to higher pressures and pick up hundreds of fps with .45 Super and other such wildcats. If you want to fit more rounds into the same carry profile almost any modern alternative can still provide higher energy, better ballistics, and less recoil.
I am very aware of the physics. I took three terms of classic physics in college at the Blue Mountain Community College while taking my calculus classes.
If you think I am wrong, then Hawks is wrong as well:
http://www.chuckhawks.com/handgun_recoil_table.htm
http://www.chuckhawks.com/shotgun_recoil_table.htm
http://www.chuckhawks.com/recoil_table.htm Rifle Recoil Table
These are unit of energy with results given in joules or ft/lbs of force.
http://en.wikipedia.org/wiki/Recoil
You seem to have an agenda. I have checked these things extensively with various sources for penetration, energy, and expansion for different brands, calibers, and weights in grains. At this point, for anyone who is unbiased, I have presented far more than enough evidence and you keep making claims and assumptions with no facts or proof. I will rest on the evidence that renders the verdict – .45 ACP is not now, or likely in the near future, to be obsolete. My subscription ends here.
You are confusing “recoil energy” with momentum.
Recoil energy is useful in describing what a shooter “feels” shooting a specific round in a specific gun because it incorporates the mass of the gun, which dampens the recoil momentum. However the purpose of my argument was to take the particulars of a gun out of the equation so we could focus on the technical merits of the cartridges. That’s why I have been talking about momentum. You can always reduce recoil energy by increasing the weight of the gun; just like you can to a great degree increase muzzle energy by increasing barrel length. (This is also why the major handgun shooting sports, after constraining the weight, size, and muzzle devices of permitted guns, use a momentum measure like “Power Factor” to segregate their classes of competition.)
My approach is actually quite practical: Suppose you are shopping for a handgun. You might first narrow your choice to a particular style and brand — e.g., Glocks or Sigs. You will also pick a profile — e.g., full-size, compact, or sub-compact. At that point you’ve determined the barrel length and weight of the gun, and you can choose from a range of calibers, including those I listed initially. Now, if you read and understood what I have written here, .45 ACP would probably be the last caliber you would choose.
Don’t forget .38 Super: As powerful as .357 SIG, more common, and smaller 9mm case diameter = higher magazine capacities.
Good point. Although at least in domestic factory ammo it’s not as common as .357 SIG .38 Super outperforms .45 ACP in a 9x23mm case — just .15″ longer than 9mm Luger (9x19mm). In handgun sports the 9x23mm variants appear quite frequently because of their magazine capacity, pressure, and recoil advantages over .45 ACP.
Pingback: EmptorMaven » Blog Archive » Clarification on Ultralight Bullet Ballistics
Case Closed: FBI Says 9mm Is The Best Pistol Round.
In many ways what you say in your report is correct. With modern hollow point ammo, the power disparity gap between 9mm and .45acp has been reduced by a significant amount. The same advancement in the rounds design that increase the 9mm effectiveness also aid the .45, but not to the same degree.
The 9mm is certainly a credible service/defensive caliber. It is lighter but does have a higher velocity then the .45, and the formula for kinetic energy is (velocityx2 +mass). which means velocity does have twice impact for the amount of kinetic energy potential then mass does. A major factor in the effectiveness of a bullet impact is in its ability to transfer this energy and modern hollow points greatly aid in this.
Having said that, and after a lot of research, I favor the .45 acp. The reason is that the 9mm lives and dies by its velocity, and expansion. these are not constant variables also, the .45 carries approx. 75 % more mass and travels roughly 90 % of the 9mm velocity. The increased weight (a constant factor) reduce the chance that the round will fail to adequately penetrate the target, and its increased diameter (a constant factor) aids in transfer of kinetic energy even in the event the round fails to expand properly.
In gel testing you can see that the 9mm “runs out of gas” very quickly and its “stretch cavity or cavitation” ends in 5-7 inches typically, as it lacks the momentum of weight. This may or may not be deep enough to impact vital organs if the round doesn’t actually pass through them. the .45 has a much broader, longer wound channel. Also,gel tests typically don’t factor in the many different variables found in human tissue (bone, tissue density, etc).
I like to have the least number of things that could cause failure when choosing a defense cartridge. I believe the 9mm caliber is effective if it performs as intended and one day the technology in ammo manufacturing will eliminate the possible short comings in the 9mm (I own that caliber as well) but I don’t think it has happened yet.
just ran across this…interesting arguments on both sides. to the final comment above, the equation for Kinetic energy is NOT velocityx2 + mass. It is 1/2 mass times velocity squared. So the velocity is does not have twice the impact….it has exponentially more impact.
moreover, many other factors are left out of all equations above when it comes to lethality or stopping power
angle of incidence, tumbling, structures encountered etc. will make more than make up the disparity between stats listed in either direction
also the charts listing the number of rounds fired for incapacitation leaves out a vital statistic which is the distance at which those rounds were fired—often the smaller ones are ONLY fired at very close distances which of course lends to less rounds needed due to better placement….so this invalidates the chart for the relevant discussion at hand as to effectiveness of one round over another with all other things being equal
No one has once factored in “shock” abosrorption or “knock down” power if you will which basically stuns or knocks out the enemy. The .40 and .45 are the best at this hands down compared to the 9mm leaving most wounded and left to come back and take your butt to court. Case closed. Don’t need an enemy to get back up. Point made!
And also, personally going from a 9mm which is much more ear piercing than the low wave .45acp I have also found the recoil much less “snappy” and painful when shooting a .45acp even in 3.” Shooting a .380 is like getting poked with a pin where as shooting a .45 acp is like getting shoved by a beer can or something like that. It hurts less. And getting back to target acquisition is much easier with the .45acp. You guys at basing everything on numbers. I base my facts on shooting 100 rounds of 230gr .45 and by far the most comfortable pistol to shoot is the .40 HK P30 V1 LEM! Best in the book!
Unless you are planning on walking around with ear plugs I suggest the 4″ bull barrel .45 acp. Or make a commander yourself and use good parts. I made my own and haven’t had one failure from day one and that was years ago. It’s crazy what mass production has done to quality. Very sad times these are. It’s so easy to make a $5000 1911 that shoots better and fits better than any mass produced “top of the line anything” because they don’t have the time put into them that’s needed to not have failures. By far the worst gun I shot was a Sig P232 .380, so snappy and it would constantly FTE and stovepipe unless you held it rock solid. Trust that? No thanks sir!
What was meant by $5000 1911 was that on the market it would cost that to buy, but around $1400 to make.
There are some major problems with the comments here. One is that John Lloyd Scharf was attempting to, and was partially successful at turning this discussion into simply a “.45 vs 9mm” argument. I believe he did this intentionally…picking on the least powerful of the listed cartridges. He also chose some relatively obscure example-load for the .45 acp, comparing it to conventional (sometimes police-issued) 9mm loadings. Again I believe this was intentional. Comparing conventional loads for ALL the cartridges Fully supports the original claim the the .45 acp has been rendered obsolete. The .45 doesn’t have to be Ineffective to be obsolete. If the power of typical loads is at least Similar to the .45acp, while the capacity in a certain size firearm is Greatly Dissimilar…again the original contention is supported that the .45 acp is obsolete. For the sake of argument lets look again at the “9mm vs .45acp” debate…even though the 9mm is NOT my number one choice for self-defense. Comparing the .45 acp to the 9x19mm indeed gives the .45 its BEST chance to shine among popular defensive cartridges.
9mm 124gr@1181fps produces energy of 384ft-lbs
.45acp 230gr@875fps produces energy of 391ft-lbs
These energy levels are indeed similar. The recovered diameter of the respective projectiles vary by manufacturer and design but they are at least Similar among the best loads at these energies. BUT…
What is Greatly Dissimilar is the capacity of similar sized firearms!
A pistol such as the 9mm aprox. 4inch barrel Glock 19 carries 15+1rounds for a total of 16.
A similar sized pistol in .45 acp, an aprox. 4inch barrel 1911 etc. carries typically no more than 8rounds in its standard magazine.
This fact supports the contention that the .45 acp is obsolete. Not Ineffective mind you, but obsolete in terms of being inefficient is terms of size and weight, and also felt recoil, for a given level of total energy-delivery. When we consider the standard-pressure loadings of the more modern cartridges such as .40 S&W, .357Sig, and 10mm Auto the argument only becomes stronger against the Superiority of the .45 acp.
I personally prefer .40 S&W currently, and prefer listed energy levels above 500ft-lbs with bullet weights of 135 or 155grains. My choice is based on factors such as ammo capacity, power, availability, price, and my comfort firing the ammo from a completely unmodified Glock 23…among other reasons. I feel comfortable with the level of energy. I feel comfortable with the size of the rounds fired. I don’t fear a lack of expansion partially because I have seen tests in which 165grain FMJ (FMJ!) rounds Expand/Mash-up on impact. Also,my extra capacity over most .45 acp pistols does not Force me to fire a large number of rounds! However…the limited capacity of similar-sized .45 acp pistols does indeed Prevent me from firing a large number of rounds.
Your Mileage May Vary,
Thank you.
John Lloyd,
The 45 ACP was designed as a “man stopper” when we were fighting the Moros jacked-up on opium and strapped with tourniquets wielding big knives… it was tested on pigs, goats, and sheep, using very subjective criteria. Once Martin P. Fackler and Dr’s. Courtney and Courtney came along… all the subjective glory and folk-lore was put to bed.
The 9mm was designed to replicate the 38… a round which was designed as a man-killing round.
Let’s take a look at what professional killers use… virtually every military around the world has transitioned to a 9mm of one sort or another… including the Soviet Block nations using the Makarov with its 9mm X 18mm cartridge. Even John Browning followed the 1911 with the High Power. The SEALS, CIA, FBI, and multiple US Government agencies abandoned the 45 ACP for the 9mm’s ultimately superior over-all usability. The super-charged .38 round known as the .357 Magnum, trumps the 45 ACP across the spectrum… if the round’s performance is your priority and round-count isn’t important to you… then, you should be carrying a revolver.
The 1911 proved less accurate, less reliable, harder to maintain, and more prone to malfunctions under adverse conditions than multiple competitors during the DoD’s side-arms competition of the 1980’s. Part of it is the slip-fit tolerances between the muzzle, barrel, and slide. The 5″ barrel increases the sight-base of the 1911… but, put the same effort and money used to create a highly-accurate 1911 with a great trigger into some other brands, and you’ll have a FAR superior pistol.
It’s o.k. John, you can still love your Colt, your Harley, and your ’57 Chevy Belair… but, the fact is, there are lots of superior-performing options to all of them.
since other folks are commenting on this zombie article I figure I would too.
Nealry all points above are pretty accurate on bother sides. That said people are confusing a few things. Stopping power is not muzzle energy. Stopping power is much more difficult to quantify and aspects such as momentum come into play as energy has to be transferred into the receiving object while maintaining sufficient levels of penetration, and while creating a big enough wound.
Now… energy… in the equations above we’re talking about E = 1/2 m x v^2… this equation favors higher velocities, which favors the smaller rounds. That said momentum is P = MV which, if you do some bullet math, actually favors the mass. This creates an interesting and unresolved dynamic where 45 acp wins the momentum side of the equation but loses (generally) the energy side of the equation. I don’t think you can say definitively that any of the 3 main defensive rounds any is better or best at “stopping”.
Another thing that I think is crucial to the argument is non-expanding HP rounds. Civilian ballistics revolve around hollow points where military and most police departments use FMJ. Hollow point ammo does not always open up like it’s supposed to and an unopened HP round will transfer significantly less energy to the receiver if it over penetrates, and over penetration poses serious threats to innocents in home defense. This is an area that 45 ACP does still reign supreme in. It’s simply larger and more massive, and because of that it transfers more energy to the receiver if a HP is un-expanded. This coupled with it’s typically slower velocities means it is also less likely to over penetrate if a HP does not open (a much desired quality in home defense).
In the end I think the 45 is still a viable option because of the above characteristics and I believe labeling it “obsolete” is a bit of an overreach.
As the owner of both a .45 and a 9mm I fail to understand why those who like either caliber can’t buy what they want and leave it at that I get along with both of mine each has its own place
(The bigger the nail the bigger the hammer should be)
Emptor Maven and to all those reading his report – After reading the key parts of your article here,(although this was from Feb 2013, this appears to me to be a very biased report. You use high power cartridges for almost ALL the comparisons, and ignored any +P 45 ACP cartridges. You also ignored the fact that the military is reconsidering going back to the 45 ACP over the current 9mm, mainly due to the reports from actual field usage where they need MORE stopping power, which the 45 ACP does nicely. So, you have misled a lot of people with your report, and indeed the military is really thinking of going back to what you call the ‘Obsolete 45 ACP’.
If you are still there, and what a real caliber comparison, which includes the 45 ACP and 9mm (to some extent), email me at vlavalle@ix.netcom.com and I will send you my Excel ballistics file. This shows mainly hand gun calibers (and a few rifle and larger military guns & cannons), and mainly revolver type ammo for the hand guns, since I have two Ruger Black Hawks. In this file, it lists the ballistics for all the listed ammo, where you can order it online and for how much, and a price per cartridge column as well, and even some ammo pictures.
Your comment about 45 ACP being much more costly than 9mm is not correct either! It is somewhat more, but nothing really large or enough to deter anyone away from it. But your comment about not being able to carry a large load in the mag is true, and also very obvious, and is probably why the military decided to go with the 9mm in the ’80’s when there was No war, and no one to really consider what that meant to the guys in action. Now that we have been thru 2 wars and much scrimmaging, the field reports are coming back that the 9mm is not cutting it!
If you look at this Excel file, you will see that the average of the 9mm ammo I have listed vs. the average of the 45 ACP is drastically different, and the 45 ACP for this average is 20% more powerful (ft. lbs.). Also, the MOST powerful 9mm I have found (+P) is 465 (much more powerful than what you showed in your article), whereas the most powerful 45 ACP (+P) is 616 (185 gr) or 625 (78 gr).. So, there is NO question empirically about which has more power’ Furthermore, since the 45 CP is 28% larger in width, it has even much more stopping power.
Vincent (12-29-2015)
.
Again, lets PLEASE try to refrain from hijacking this subject and turning into simply “9mm vs. 45acp”! I understand why this is happening but it is wrong to do so.
Instead for now let’s compare the ballistics of the 10mm Auto. John Lloyd Scharf found an obscure manufacturer of ammunition, “Atomic Ammo” brand, that produces a 185grain .45acp round with 616 ft-lbs of energy at the muzzle. We can compare this favorably with a long-standing, well-known manufacturer with a very popular bullet. Winchester has Silvertip ammo in 10mm Auto of 170 grains at a speed of 1290 fps resulting in 649 ft-lbs. From a well-respected maker of ammo!! Indeed it is superior to the “specialty” 45acp load! When we compare this standard 10MM SILVERTIP to standard .45ACP SILVERTIP ammo the difference in power is even more apparent. The .45acp Silvertip load is pushing an 185grain bullet at 1000fps resulting in 411 ft-lbs of energy. Same manufacturer, same bullet…but Vastly different performance between the two calibers. Added to that is the fact that the 10mm will hold more of these more-powerful rounds in a given sized package! Even comparing the “Atomic Ammo” brand, the 10mm is more powerful AND holds more rounds! Also the increased velocity increases the likelihood of expansion over even that non-typical .45acp round.
Comparing the more common 411 ft-lb .45acp Silvertip with other calibers’ common loadings is even more telling. The Winchester Silvertip 155grain .40s&w produces 500 ft-lbs at a velocity of 1205fps. Again this is more energy than the .45acp and again also that is with more of the more-powerful rounds held in the gun! Even considering the lowly 9mm…the Silvertip load has 383ft-lbs which is indeed a small bit less than the 411ft-lbs of .45acp, but again it is only slightly less. And it is in a smaller package allowing for approx. TWICE the number of rounds to be carried in the gun. I wasn’t able to find stats for a Winchester Silvertip .357sig loading, but I found that Winchester loads a JHP of 125 grains moving at 1350fps for an energy figure of 506ft-lbs. Capacity would be the same as .40s&w.
Speaking of the .40, the VAST majority of common .40s&w loadings are superior to 411ft-lbs and 1000fps. The same is true for .357sig loadings. 9mm+P rounds commonly surpass this figure also.
.45acp+P rounds are INDEED capable of decent power, but it comes at the expense of greater recoil…and once again, the capacity of the firearms are still lacking when compared to the more-modern calibers.
No one…at least not me…ever said that the .45acp, particularly with +P loads, was INEFFECTIVE. It is simply true that the .45acp is OBSOLETE when power is considered along with size, capacity, weight and recoil. There are simply Better Options available! But many, MANY advocates of the .45acp vehemently refuse to even Consider the possibility that the .45acp “might” not be the best. Some evidence of this is in John Lloyd Sharf’s (and others’) eagerness to restrict the discussion to only “9 versus 45”.
If you already have a .45acp pistol and can shoot it well, that is a good thing! I legitimately and sincerely hope you don’t ever Need to “use it”…and if you do I hope you don’t ever need more ammo than you have!!!
But to new gun buyers I hope that you at least Consider some of more modern calibers that offer legitimate advantages over pistols chambered in .45ACP.
Thank You.
The “more powerful” rounds are not more effective in a firefight. I gave many proofs of this. The point of a .45 is not its ability to drive holes in objects. There is no such thing as one shot/one kill, particularly from anything other than a rifle or a shotgun. When it comes to a 45, they have remarkably less recoil and chance of over-kill. When an officer fires ten times and runs over 100 feet to stop an unarmed 18 year old in Missouri, do not claim they are more potent in stopping power.
I purchased a 45 with a 5 inch barrel because it was simply more comfortable to fire. I found it had less snappy recoil and allows me to acquire my target again more quickly than 9’s and 40’s. There are different ways to argue ballistics based on size and load of bullets. I went it to this with an open mind and chose the 45. It’s a bigger bullet so a bigger hole. I say use what you shoot most accurately….. that’s most important…..
Stopping power will always be trumped by shot placement. .45, .357, 9mm, or .40….doesn’t matter what you shoot as l9ng as you can accurately place those rounds where they need to go when the time comes. 12″ is the average width of a man’s body. The permanent cavity created at the 6″ mark is probably the most important thing to consider. Under penetrarion is just as bad as over penetration.
I would only disagree about over-penetration. If it goes through the aggressor and hits any innocent party, over-penetration is more important than under penetration. If I make an inch wide hole from 9 feet with an aggressor, I am not too concerned about how deep it goes.
It’s an excellent round for suppression. The best pistol calibers for suppression are .45 acp and 22lr. The only pistols I have cans for. I tend to carry my 9mm for EDC more often then my compact .45.
@Darwin – Good point! Low-pressure, low-velocity rounds are ideal for suppressed shooting, so that’s an argument for the relevance of .45ACP.
I disagree with John Lloyd Scharf that “there is no such thing as one shot / one kill”, but his assertion brings up the valid point that the .45 acp does INDEED offer the Least chances at a head shot among the major calibers mentioned! Lucas seems to concur above with the contention that shot placement trumps “stopping power”. The .45 acp offers the least chances for effective shot placement among popular calibers within a given size.
An issue was raised regarding suppressed firearms. This brings to mind the fact that the .40 S&W does indeed offer 180grain rounds at subsonic velocities, while the SAME .40 S&W caliber has highly effective supersonic offerings with bullets of reliably-expanding lighter weights. And again this is with more bullets within a given-size platform. It seems to be a more versatile round when these things are considered.
In regards to recoil comparisons…I personally prefer a “snappy” recoil that is quickly over-and-done-with, as opposed to a long drawn-out “push” of a recoil that proponents of the .45 acp indicate is common with that caliber. For me it allows me to realign my sights sooner, as my recoil would be complete while the .45 would still be pushing.
An issue has also been raised in regards to penetration depth. Many favor the FBI standard. My thoughts on this are that, while my preferred .40 S&W load penetrates 10.5 inches at very CLOSE range, due to rapid expansion…this same load will penetrates MORE at a slightly longer distance due to drops in impact-velocity. This increased penetration should satisfy the FBI requirements at the reduced velocity/increased distance. My feeling is that at close range the rapid expansion won’t be a major problem because rounds could more-reliably be directed towards head/neck/upper torso shots. This same rationale should apply also to .357magnum/sig rounds as well as 10mm and other high-speed rapid-expanding rounds. John Lloyd Scharf himself has pointed out using the .22LR example that the Penetration increased when velocity decreased!
I never said, “John Lloyd Scharf himself has pointed out using the .22LR example that the Penetration increased when velocity decreased!”
To John Lloyd Scharf: Yes sir Indeed you did! I quote below:
John Lloyd Scharf
June 13, 2013 at 2:16 am
In all those ballistic gel pictures, the fact is they can fail to expand. This is particularly so in the case of short barrel revolvers were . In fact, a pistol shot of a .22 Stinger penetrates over 18 inches because it fails to expand, yet is less than 12 inches when forced to expand by hypersonic velocities.
END QUOTE.
In this quote you clearly indicate that, in this case regarding the .22 Stinger ammo, the increased “hypersonic” velocities Decreased penetration to 12 inches…as opposed to the Increased penetration of 18 inches exhibited at the decreased velocities attained when the same round was fired from a revolver with a short barrel.
The expansion causes the decreased penetration; NOT the increased velocity. I did not say it was the velocity, which logic and common sense would tell you. I was referring to a HOLLOWPOINT .22LR, NOT ALL .22LR.
Do not blame me for your improper inference.
I don’t believe I made an improper inference at all! Immediately above you say/claim, and I QUOTE:
John Lloyd Scharf
April 2, 2016 at 12:14 am
The expansion causes the decreased penetration; NOT the increased velocity.
END QUOTE.
You sir even emphasized and Capitalized the “NOT”!
I will now simply re-refer to what I QUOTED previously above:
John Lloyd Scharf
June 13, 2013 at 2:16 am
… when forced to expand by hypersonic velocities.
END QUOTE.
To recap: You first said that the “hypersonic velocities” forced the projectile to expand. And now you say that the increased expansion caused the decreased penetration. Both of these statements are true by-the-way!! BUT then you added that part about “NOT the increased velocity.” Which completely contradicts the truth, and also contradicts what you said previously. And in your conclusion you claimed that I made an “improper inference”, which also is not supported by the facts.
Thank you.
Increased velocity does not cause decreased penetration, IF the bullet is not a hollow point, AGAIN. Therefore, increased velocity does not decreased penetration. Your logic is flawed.
Ok let’s stop with the insults such as “your logic is flawed” and “don’t blame me for your improper inference”. These are understandable from a human-nature point of view but they add nothing to the discussion.
Anyway MORE IMPORTANTLY…
Something I left out from my previous post, for the sake of readability and staying on topic, actually is HIGHLY APPLICABLE now thanks to your statement above.
Above you claim that, and I QUOTE:
Increased velocity does not cause decreased penetration, IF the bullet is not a hollow point,
ENDQUOTE.
However studies have been done regarding SOLID, FMJ, Hague-compliant rounds…again NON-HOLLOWPOINT! It has been shown conclusively in tests of 5.56mm FMJ rounds that penetration at Close-range velocity is LESS than penetration at 300meters, due to the decreased velocity at longer distances causing less deformation and yawing of even the Solid, Non-hollowpoint round.
That is simply a FACT sir, regardless of whether I have “flawed logic” or not!
uh, huh.
https://www.americanrifleman.org/articles/2015/4/16/throwback-thursday-the-fbi-ammo-tests/
The Yankee Marshal agrees with this post.